На відміну від стандартного відхилення - це квадратний корінь з числового значення, отриманого при обчисленні дисперсії. Багато людей протиставляють ці дві математичні концепції. Отже, ця стаття намагається пролити світло на важливу різницю між дисперсією та стандартним відхиленням.
Діаграма порівняння
| Основа для порівняння | Відхилення | Стандартне відхилення |
|---|---|---|
| Значення | Дисперсія є числовим значенням, що описує мінливість спостережень за його середньоарифметичним значенням. | Стандартне відхилення є мірою дисперсії спостережень у наборі даних. |
| Що це? | Це середнє значення квадратичних відхилень. | Це середньоквадратичне відхилення. |
| Позначені як | Сигма-квадрат (σ ^ 2) | Сигма (σ) |
| Висловлено в | Квадратні блоки | Такі ж одиниці, що і значення в наборі даних. |
| Позначає | Як далеко поширюються особи в групі. | Скільки спостережень набору даних відрізняється від його середнього. |
Визначення дисперсії
У статистиці дисперсія визначається як міра мінливості, яка відображає, як далеко розташовані члени групи. Він знаходить середній ступінь, до якого кожне спостереження змінюється від середнього. Коли дисперсія набору даних невелика, вона показує близькість точок даних до середнього значення, тоді як більша величина дисперсії означає, що спостереження дуже дисперговані навколо середнього арифметичного і один від одного.
Для несекретних даних :
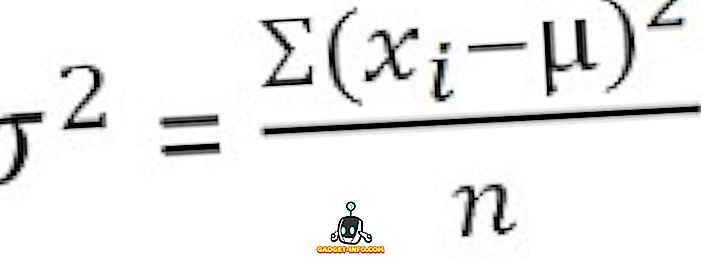
Для згрупованого розподілу частот :
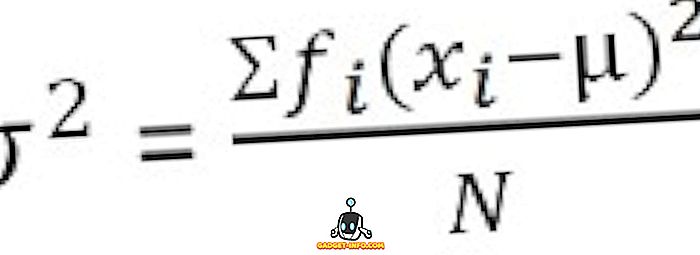
Визначення стандартного відхилення
Стандартне відхилення є показником, який визначає кількість дисперсії спостережень у наборі даних. Низьке стандартне відхилення є показником близькості балів до середнього арифметичного і високого стандартного відхилення; бали розподілені на більш високий діапазон значень.
Для несекретних даних :

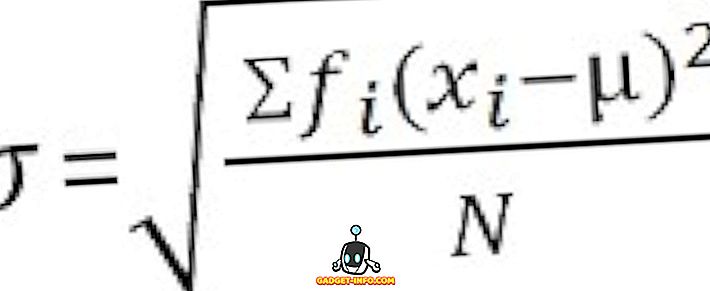
Основні відмінності між дисперсією і стандартним відхиленням
Різниця між стандартним відхиленням і дисперсією може бути зрозуміла з наступних підстав:
- Дисперсія є числовим значенням, що описує мінливість спостережень за його середньоарифметичним значенням. Стандартне відхилення є мірою дисперсії спостережень у наборі даних.
- Дисперсія - це не що інше, як середнє квадратичне відхилення. З іншого боку, стандартне відхилення - середньоквадратичне відхилення.
- Дисперсію позначають сигма-квадратом (σ2), тоді як стандартне відхилення позначають як сигма (σ).
- Дисперсія виражається в квадратних одиницях, які зазвичай більше величин у даному наборі даних. На відміну від стандартного відхилення, яке виражається в тих же одиницях, що і значення в наборі даних.
- Дисперсія визначає, наскільки поширені особи в групі. І навпаки, стандартне відхилення вимірює, скільки спостережень набору даних відрізняється від його середнього значення.
Ілюстрації
Знаки, отримані студентом у п'яти предметах, складають 60, 75, 46, 58 і 80 відповідно. Ви повинні з'ясувати стандартне відхилення і дисперсію.
Перш за все, ви повинні з'ясувати, що це означає,

Таким чином, середні (середні) оцінки становлять 63, 8
Тепер розрахуйте дисперсію
| X | A | (xA) | (XA) ^ 2 |
|---|---|---|---|
| 60 | 63.8 | -3.8 | 14.44 |
| 75 | 63.8 | 11.2 | 125.44 |
| 46 | 63.8 | -17.8 | 316.84 |
| 58 | 63.8 | 5.8 | 33.64 |
| 80 | 63.8 | 16.2 | 262.44 |
Де, X = Спостереження
A = середнє арифметичне
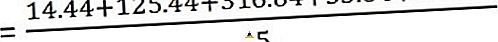
І стандартне відхилення -

Подібності
- Як дисперсія, так і стандартне відхилення завжди позитивні.
- Якщо всі спостереження в наборі даних ідентичні, то стандартне відхилення і дисперсія будуть нульовими.
Висновок
Ці два основні статистичні терміни, які відіграють важливу роль у різних секторах. Стандартне відхилення є кращим, ніж середнє, оскільки воно виражається в тих же одиницях, що і вимірювання, тоді як дисперсія виражається в одиницях, більших, ніж даний набір даних.