На відміну від цього, у випадку комбінації, порядок взагалі не має значення. Не тільки в математиці, але й у практичному житті ми регулярно переживаємо ці дві концепції. Хоча ми цього не помічаємо. Отже, уважно прочитайте статтю, щоб дізнатися, як ці два поняття різні.
Діаграма порівняння
| Основа для порівняння | Перестановка | Комбінація |
|---|---|---|
| Значення | Перестановка відноситься до різних способів упорядкування набору об'єктів у послідовному порядку. | Комбінація відноситься до декількох способів вибору елементів з великого набору об'єктів, так що їх порядок не має значення. |
| Замовлення | Відповідні | Не має значення |
| Позначає | Композиція | Вибір |
| Що це? | Впорядковані елементи | Невпорядковані набори |
| Відповіді | Скільки різних розташувань можна створити з даного набору об'єктів? | Скільки різних груп можна вибрати з більшої групи об'єктів? |
| Висновок | Кілька перестановок з однієї комбінації. | Одиночна комбінація з однієї перестановки. |
Визначення перестановок
Ми визначаємо перестановку як різні способи упорядкування деяких або всіх членів множини в певному порядку. Вона передбачає всі можливі домовленості або перегрупування даного набору в розрізняється порядок.
Наприклад, Всі можливі перестановки, створені буквами x, y, z -
- Приймаючи всі три одночасно, є xyz, xzy, yxz, yzx, zxy, zyx.
- Прийомом двох за один раз є xy, xz, yx, yz, zx, zy.
Загальна кількість можливих перестановок n речей, взятих r за один раз, може бути розрахована так:
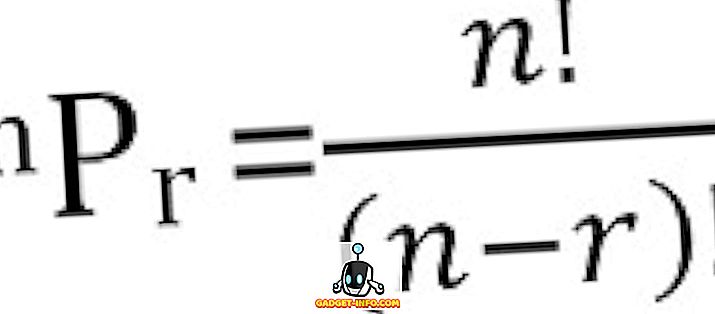
Визначення комбінації
Комбінація визначається як різні способи вибору групи, беручи деякі або всі члени набору, без наступного порядку.
Наприклад, всі можливі комбінації, вибрані з буквою m, n, o -
- Коли потрібно вибрати три з трьох літер, то єдиною комбінацією є множина
- Коли потрібно вибрати два з трьох літер, то можливі комбінації - mn, no, om.
Загальна кількість можливих комбінацій з n речей, взятих r за один раз, може бути обчислена як:
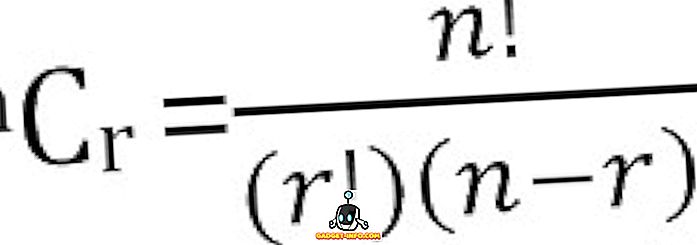
Основні відмінності між перестановкою і комбінацією
Відмінності між перестановкою та комбінацією виразно відображаються на таких підставах:
- Термін "перестановка" відноситься до декількох способів упорядкування набору об'єктів у послідовному порядку. Комбінація передбачає кілька способів вибору предметів з великого пулу об'єктів, так що їхній порядок не має значення.
- Основною відмінною точкою між цими двома математичними поняттями є порядок, розміщення і положення, тобто в згаданих вище характеристиках перестановки має значення, що не має значення у випадку комбінації.
- Перестановка означає кілька способів розташування речей, людей, цифр, алфавітів, кольорів тощо. З іншого боку, комбінація вказує на різні способи вибору пунктів меню, продуктів харчування, одягу, предметів тощо.
- Перестановка не є нічим іншим, як впорядкованою комбінацією, тоді як комбінація передбачає невпорядковані множини або сполучення значень у межах конкретних критеріїв.
- Багато перестановок можуть бути отримані з однієї комбінації. І навпаки, тільки одна комбінація може бути отримана з однієї перестановки.
- Відповіді на перестановки Скільки різних механізмів можна створити з даного набору об'єктів? На відміну від комбінації, яка пояснює, скільки різних груп можна вибрати з більшої групи об'єктів?
Приклад
Припустимо, є ситуація, коли потрібно з'ясувати загальну кількість можливих зразків двох з трьох об'єктів A, B, C. У цьому питанні, перш за все, потрібно зрозуміти, чи пов'язано це питання з перестановкою або комбінація, і єдиний спосіб знайти це - перевірити важливість замовлення чи ні.
Якщо порядок є значущим, то питання пов'язане з перестановкою, і можливі зразки будуть, AB, BA, BC, CB, AC, CA. Де, AB відрізняється від BA, BC відрізняється від CB і AC відрізняється CA.
Якщо порядок не має значення, то питання пов'язане з комбінацією, і можливі зразки будуть AB, BC і CA.
Висновок
З наведеним вище обговоренням зрозуміло, що перестановка і комбінація є різними термінами, які використовуються в математиці, статистиці, дослідженнях і в нашому повсякденному житті. Слід пам'ятати, що стосовно цих двох понять, для даного набору об'єктів перестановка завжди буде вищою, ніж її комбінація.