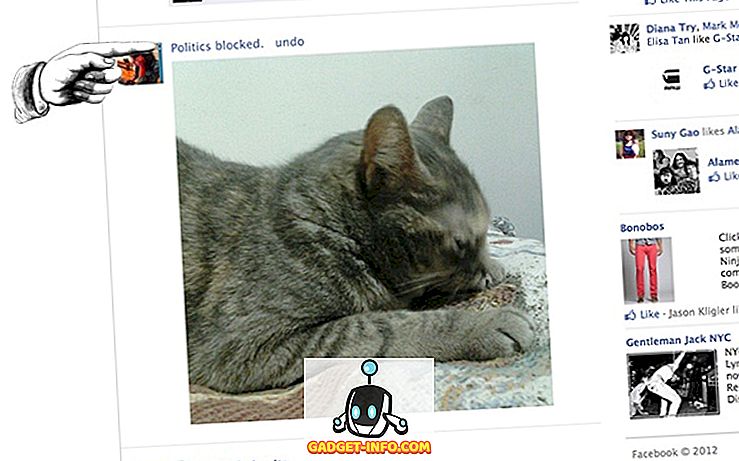
Ідеальною мірою центральної тенденції є та, яка чітко визначена, легко зрозуміла, просто обчислюється. Вона повинна ґрунтуватися на всіх спостереженнях і найменше впливати на екстремальні спостереження, що присутні в наборі даних.
Люди часто контрастують ці два заходи, але справа в тому, що вони різні. Ця стаття спеціально підкреслює основні відмінності між середнім і середнім. Гляньте.
Діаграма порівняння
| Основа для порівняння | Середнє | Медіана |
|---|---|---|
| Значення | Середнє означає просте середнє значення даного набору значень або величин. | Медіана визначається як середній номер у впорядкованому списку значень. |
| Що це? | Це середнє арифметичне значення. | Це позиційний середній. |
| Представляє | Центр тяжкості набору даних | Центр тяжкості набору даних Середній набір даних |
| Застосовність | Нормальний розподіл | Косий розподіл |
| Викиди | Середнє чутливе до викидів. | Медіана не чутлива до викидів. |
| Розрахунок | Середнє обчислюється шляхом складання всіх спостережень і потім ділення значення, отриманого з числом спостережень. | Для обчислення медіани набір даних розташовується у порядку зростання або зменшення, тоді значення, яке потрапляє в точну середину нового набору даних, є медіанним. |
Визначення означає
Середнє значення є широко використовуваним показником центральної тенденції, який визначається як середнє значення набору значень. Вона являє собою модель і найбільш загальне значення даного діапазону значень. Його можна розрахувати як у дискретному, так і в безперервному рядах.
Середнє значення дорівнює сумі всіх спостережень, поділених на кількість спостережень у наборі даних. Якщо значення, прийняте змінною, дорівнює, його значення також буде однаковим. Середнє може бути двох типів, середнє вибіркове (x̅) і середнє населення (µ). Її можна розрахувати за формулою:
- Середнє арифметичне :

n = кількість значень - Для дискретної серії :

- Для безперервних служб :

A = Передбачена середня
C = Спільний дільник
Визначення медіани
Медіана є ще одним важливим показником центральної тенденції, яка використовується для розподілу величини на дві рівні частини, тобто більшу половину вибірки, популяції або розподілу ймовірностей від нижньої половини. Це середнє значення, яке досягається, коли спостереження сортуються в певному порядку, або в порядку зростання або спадання.
Для розрахунку медіани, перш за все, організуйте спостереження в найнижчому або найвищому або найвищому до найнижчого, потім застосовуйте відповідну формулу, згідно з умовами, наведеними нижче:
- Якщо кількість спостережень непарне :

- Якщо кількість спостережень рівна :

- Для безперервних серій :

c = кумулятивна частота попереднього середнього класу
f = частота медіанного класу
h = ширина класу
Ключові відмінності між середнім і середнім
Значні відмінності між середнім і середнім значеннями наведені нижче:
- У статистиці середнє значення визначається як просте середнє значення даного набору значень або величин. Медіану називають середнім числом у впорядкованому списку значень.
- Хоча середнє арифметичне середнє, медіана є позиційною середньою, по суті, положення набору даних визначає значення медіани.
- Середній визначає центр тяжкості набору даних, тоді як медіана висвітлює середнє значення набору даних.
- Середнє значення є прийнятним для нормально розподілених даних. З іншого боку, медіана найкраща, коли розподіл даних перекошений.
- Середнє значення сильно впливає на екстремальне значення, яке не має місце у випадку з медіаною.
- Середнє значення обчислюється шляхом підсумовування всіх спостережень, а потім ділення значення, отриманого з числом спостережень; результат є середнім. На відміну від медіани, набір даних розташовується в порядку зростання або зменшення, тоді значення, яке потрапляє в точну середину нового набору даних, є медіаною.
Приклад
Знайти середнє значення та медіану даного набору даних:
58, 26, 65, 34, 78, 44, 96
Рішення: Для обчислення означає, що потрібно розділити суму спостережень на кількість спостережень,

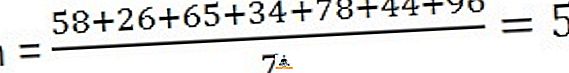
Для обчислення медіани, перш за все, розташуйте рядки в послідовності, тобто найменші до найвищих,
26, 34, 44, 58, 65, 78, 96
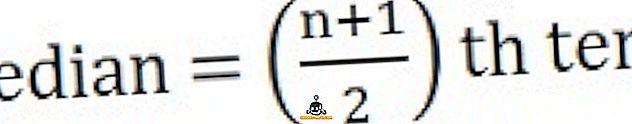
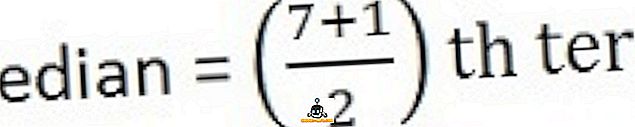
Висновок
Розглянувши наведені вище пункти, можна сказати, що ці дві математичні поняття різні. Середнє арифметичне або середнє вважається найкращою мірою центральної тенденції, оскільки містить всі ознаки ідеальної міри, але має один недолік, що коливання вибірки впливають на середнє значення.
Таким же чином, медіана також однозначно визначена і легко зрозуміти і обчислити, і найкраще в цьому вимірі, що вона не залежить від коливань вибірки, але єдиним недоліком медіани є те, що вона не заснована на всіх спостереження. Для класифікації з відкритим кінцем, медіана, як правило, краща за середню.