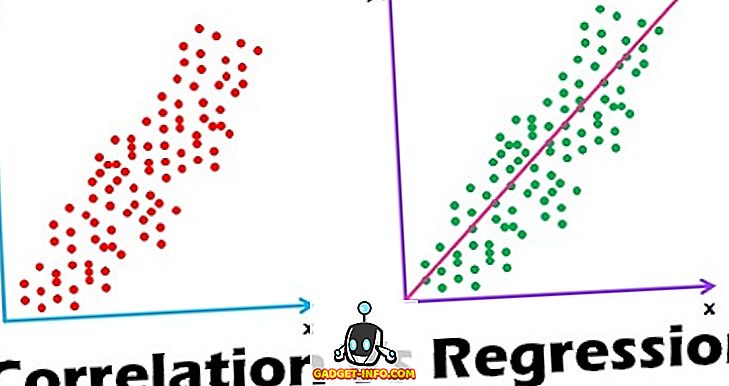
Різниця між кореляцією та регресією є однією з найпоширеніших питань в інтерв'ю. Більше того, багато людей відчувають неоднозначність у розумінні цих двох. Отже, прочитайте повну статтю, щоб мати чітке розуміння цих двох питань.
Діаграма порівняння
| Основа для порівняння | Кореляція | Регресія |
|---|---|---|
| Значення | Кореляція - це статистичний показник, який визначає взаємозв'язок або асоціацію двох змінних. | Регресія описує, як незалежна змінна чисельно пов'язана з залежною змінною. |
| Використання | Для представлення лінійної залежності між двома змінними. | Щоб підібрати кращу лінію і оцінити одну змінну на основі іншої змінної. |
| Залежні та незалежні змінні | Без різниці | Обидві змінні різні. |
| Позначає | Коефіцієнт кореляції вказує на ступінь зміщення двох змінних. | Регресія вказує на вплив зміни одиниці у відомій змінної (x) на оціночну змінну (y). |
| Мета | Знайти числове значення, що виражає взаємозв'язок між змінними. | Оцінити значення випадкової величини на основі значень фіксованої змінної. |
Визначення кореляції
Термін кореляція - це комбінація двох слів "Co" (разом) і відношення (з'єднання) між двома величинами. Кореляція полягає в тому, що під час вивчення двох змінних спостерігається, що зміна одиниці однієї змінної відповідає еквівалентною зміною іншої змінної, тобто прямою чи непрямою. Або ж змінні вважаються некоррелированними, коли рух в одній змінній не дорівнює жодному переміщенню в іншій змінної в певному напрямку. Це статистичний метод, який представляє силу зв'язку між парами змінних.
Кореляція може бути позитивною або негативною. Коли обидві змінні рухаються в одному напрямку, тобто збільшення однієї змінної призведе до відповідного збільшення іншої змінної і навпаки, тоді змінні вважаються позитивно корельованими. Наприклад : прибуток та інвестиції.
Навпаки, коли дві змінні рухаються в різних напрямках, таким чином, що збільшення однієї змінної призведе до зменшення іншої змінної і навпаки, ця ситуація відома як негативна кореляція. Наприклад : ціна і попит на продукт.
Заходи кореляції наведені як:
- Коефіцієнт кореляції продукту-моменту Карла Пірсона
- Коефіцієнт рангової кореляції Спірмена
- Діаграма розкиду
- Коефіцієнт паралельних відхилень
Визначення регресії
Статистична методика оцінки зміни залежної змінної метрики внаслідок зміни однієї або декількох незалежних змінних, заснована на середньому математичному відношенні між двома або більше змінними, відома як регресія. Вона відіграє важливу роль у багатьох видах діяльності людини, оскільки вона є потужним і гнучким інструментом, який використовувався для прогнозування минулих, нинішніх або майбутніх подій на основі минулих або нинішніх подій. Наприклад : на основі минулих записів можна оцінити майбутній прибуток підприємства.
У простій лінійній регресії існують дві змінні x і y, де y залежить від x або say, на яку впливає x. Тут y називається залежною або змінною критерію, а x є незалежною або предикторною змінною. Рядок регресії y на x виражається як:
y = a + bx
де, a = постійна,
b = коефіцієнт регресії,
У цьому рівнянні a і b є двома параметрами регресії.
Основні відмінності між кореляцією та регресією
Наведені нижче пункти пояснюють різницю між кореляцією і регресією в деталях:
- Статистична міра, яка визначає взаємозв'язок або асоціацію двох величин, відома як кореляція. Регресія описує, як незалежна змінна чисельно пов'язана з залежною змінною.
- Кореляція використовується для представлення лінійної залежності між двома змінними. Навпаки, регресія використовується, щоб відповідати кращій лінії і оцінювати одну змінну на основі іншої змінної.
- У кореляції не існує різниці між залежними і незалежними змінними, тобто кореляція між x і y подібна до y і x. І навпаки, регресія y на x відрізняється від x на y.
- Кореляція вказує на силу асоціації між змінними. На відміну від, регресія відображає вплив зміни одиниці на незалежну змінну на залежну змінну.
- Кореляція спрямована на знаходження числового значення, яке виражає взаємозв'язок між змінними. На відміну від регресії, метою якої є передбачити значення випадкової величини на основі значень фіксованої змінної.
Висновок
З урахуванням вищевикладеного, очевидно, що існує велика різниця між цими двома математичними поняттями, хоча ці два досліджуються разом. Кореляція використовується, коли дослідник хоче знати, чи є співвідношення досліджуваних змінних чи ні, якщо так, то яка сила їхньої асоціації. Коефіцієнт кореляції Пірсона розглядається як найкращий показник кореляції. В регресійному аналізі встановлюється функціональний зв'язок між двома змінними, щоб зробити майбутні прогнози щодо подій.